The Self-attention mechanism as shown in the paper is what will be covered in this post. This paper titled ‘A Structured Self-attentive Sentence Embedding’ is one of the best papers, IMHO, to illustrate the workings of the self-attention mechanism for Natural Language Processing. The structure of Self-attention is shown in the image below, courtesy of the paper:
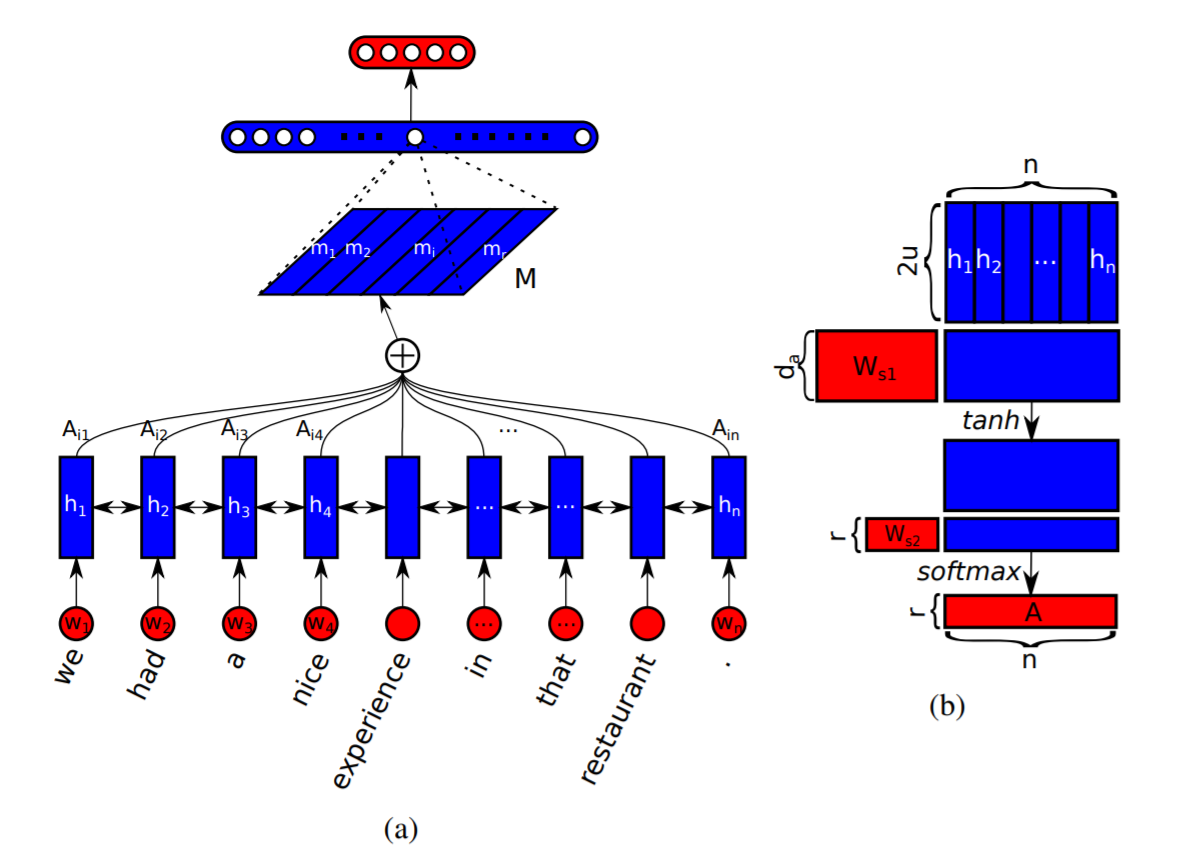
Suppose one has an LSTM of dim ‘u’ and takes as input batches of sentences of size ‘n’ words. Each sentence can be represented as
$$
S = (w_1, w_2,....w_n)
$$
where each word is the result of and has a size corresponding to the output size of the embedding layer before it. The output of the hidden layer for a bidirectional LSTM is (n x 2u). $$h^{\rightarrow}_t , h^{\leftarrow}_t $$ both have a size of 'u' that is concatenated to get the bidirectional hidden state $$h_t$$ of size '2u'. For each 'n' word there is a corresponding hidden state, therefore we can can write a hidden state matrix 'H' of dimension (n x 2u) as
$$
H^T = (h_1, h_2....h_n)
$$
Now if we want to compute a vector of attention weights given by 'a', according to the paper we can compute this vector using the following formula
$$
\bold{a} = softmax( \bold{w}_{s2} \cdot tanh( \bold{W}_{s1} \cdot \bold{H}^T))
$$
where $$\bold{W}_{s1}$$ is a weight matrix of shape (d x 2u) and $$\bold{w_{s2}}$$ is a weight vector of shape (1 x d). Here 'd' is a hyperparameter that can be set at runtime. The two weight matrices are parameters whose values are updated during the training process. Now if we work through the equations, we can see the dimensionality of each component that is displayed in square brackets next to each term below.
$$
\bold{W_{s1}} [d \times 2u] \cdot \bold{H}^T [2u \times n] = \bold{X} [d \times n]
$$
$$
\bold{Y} = tanh(\bold{X}) \longrightarrow \bold{W}_{s2} [1 \times d] \cdot \bold{Y} [d \times n] = \bar{\bold{Y}} [1 \times n]
$$
$$
\bold{a} = softmax(\bar{\bold{Y}}) [1 \times n]
$$
This ensures that the attention vector of weights 'a' is normalized. We can compute the scaled attention vector 'm' as shown below
$$
\bold{m} [1 \times 2u] = \bold{a} [1 \times n] \cdot \bold{H} [n \times 2u]
$$
The calculations are computed for each focus area in a sentence, this area of focus could be a phrase or it could be a word. In our work, we almost always assume the focus area is a word which implies that 'n' attention vectors of weights can be computed which transforms the scaled vector 'm' to a matrix 'M'. For the sake of generality, let us assume that we have 'r' focus areas in a sentence such that 'r' = 'n' for the specific case mentioned above. In literature, each pass over the focus areas is called a hop.
So how does this affect our terms that we discussed above.
Instead of a vector of weights for ‘a’ we get a matrix ‘A’ of size (r x n). This results from the following change to the weight vector
$$
\bold{w_{s2}} [1 \times d] \longrightarrow \bold{W_{s2}} [r \times d]
$$
and the resulting scaled attention vector 'm' becomes the scaled attention matrix 'M'
$$
\bold{m} [1 \times 2u] \longrightarrow \bold{M} [r \times 2u]
$$
since
$$
\bold{A} [r \times n] \cdot \bold{H} [n \times 2u] = \bold{M} [r \times 2u]
$$